10. Декартово произведение множеств

---

ВПЕРЁД ⇒

Отношение с n аргументами на множестве

⇐ НАЗАД

Задание множества при помощи его элементов

---

Декартово произведение множеств

Ранее мы рассматривали такие упорядоченные $n$-ки $⟨x_1,x_2,...,x_n⟩$, элементы в которых принадлежат одному и тому же множеству $X$. Но ничто нам не запрещает рассмотреть более общую ситуацию, когда элементы в упорядоченных наборах принадлежат различным множествам. Например, мы можем рассматривать следующие упорядоченные наборы для элементов из множеств $A$, $B$ и $C$:

$$\begin{array}{rl}⟨a_1& ,b_1,c_1⟩\\ ⟨a_1& ,b_2,c_3⟩\\ ⟨c_k& ,b_l,a_m⟩\\ ⟨a_1& ,a_1,a_1⟩\\ ⟨b_2& ,b_2,b_{10}⟩\end{array}$$

и т.д.

Рассматривая приведённые выше примеры упорядоченных наборов, можно сделать вывод, что позиции упорядоченного набора являются независимыми друг от друга, то есть каждая из позиций может обладать своим собственным правилом размещения элементов в данной позиции. Например, для упорядоченной пары можем условиться, что в первой позиции могут располагаться только элементы из множества $A$, во второй - только элементы из множества $B$. Или, например, можем условиться, что во всех позициях упорядоченного набора можно независимо друг от друга размещать элементы только одного множества $X$, причём размещаемые элементы могут дублировать друг друга в различных позициях упорядоченного набора.

Учитывая предыдущую информацию, перейдём теперь к рассмотрению упорядоченной $n$-ки (то есть упорядоченного набора, состоящего из $n$ элементов). Условимся, что элементами упорядоченной $n$-ки могут являться только элементы из множества $X$. Мы хотим перебирать всевозможные комбинации расположения элементов множества $X$ в упорядоченной $n$-ке и помещать получаемые таким образом упорядоченные $n$-ки в новое множество $Y$. Будем обозначать полученное таким способом множество $Y$ через выражение "$X^n$". Таким образом, $X^n$ - это множество всех упорядоченных $n$-ок, состоящих из элементов множества $X$.

Что будет с множеством $Y$ при $n=1$? Подставим значение $n$ в выражение для множества $Y$: $Y=X^n=X^1=X$. Справедливо ли такое утверждение? Да, справедливо. Если $n=1$, то любая из упорядоченных $n$-ок, входящих в множество $Y$, состоит только из одного элемента, принадлежащего множеству $X$. Таким образом, множество $Y$ содержит все возможные комбинации одиночных элементов из множества $X$, то есть $Y=\{⟨x_1⟩,⟨x_2⟩,...,⟨x_n⟩\}=\{x_1,x_2,...,x_n\}=X$.

Примечание

$X^n$ называется $n$-кратным декартовым произведением $X$ на себя, или $n$-й декартовой степенью множества $X$.

Если $Y$ и $Z$ - множества, то $Y\times Z$ означает множество всех таких упорядоченных пар $⟨y,z⟩$, что $y\in Y$ и $z\in Z$.

Примечание

$Y\times Z$ называется декартовым произведением множеств $Y$ и $Z$.

Аналогично, $Y\times X\times ...\times Z$ называется декартовым произведением множеств $Y$, $X$, …, $Z$.

Декартово произведение множеств можно легко объяснить на примере прямоугольной системы координат.

Прямоугольная (декартова) система координат - прямолинейная система координат со взаимно перпендикулярными координатными осями на плоскости или в пространстве.

Рассмотрим декартову систему координат для двумерного пространства (т.е. плоскости).

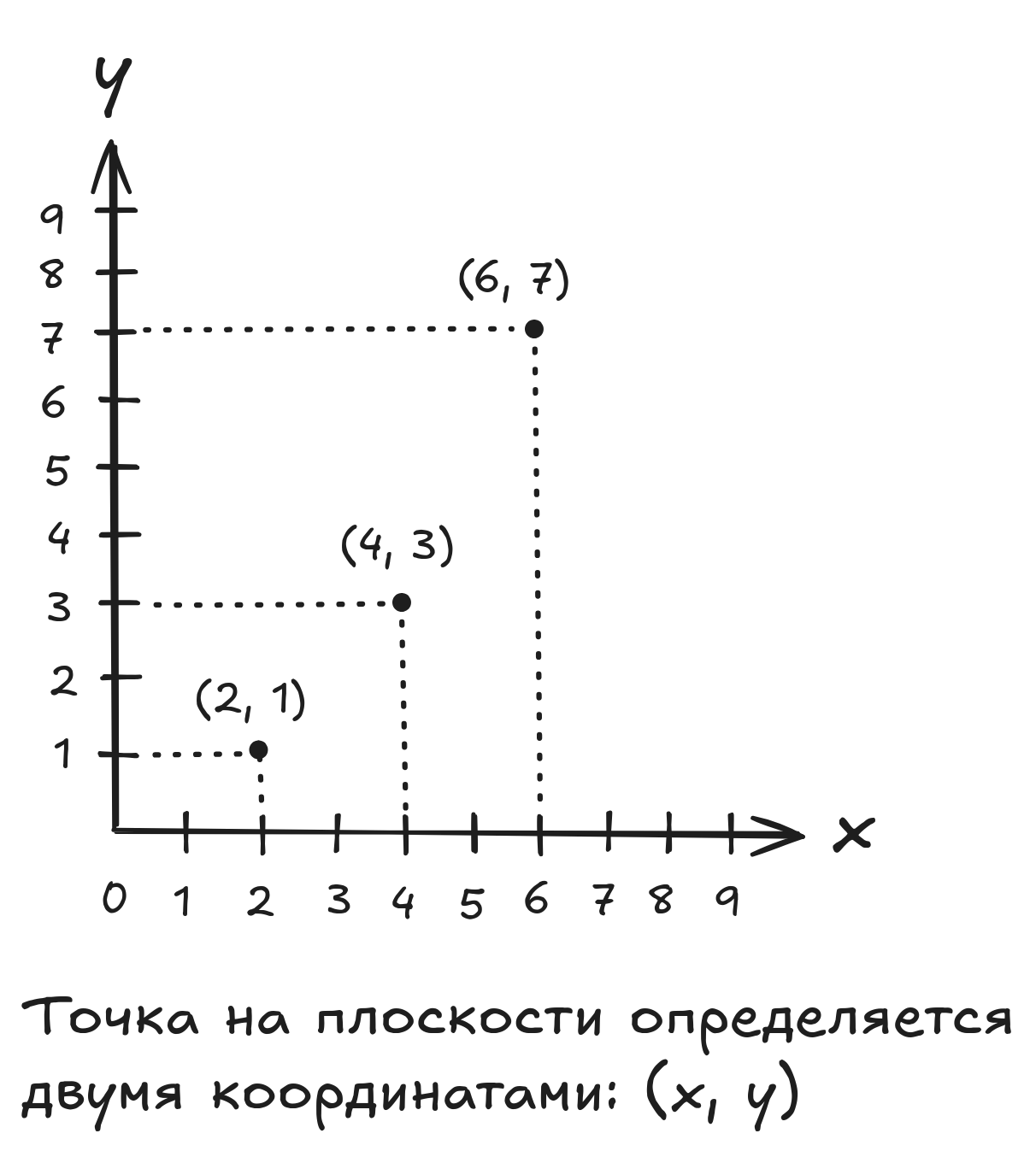
Пусть даны два множества $X$ и $Y$. Декартово произведение множества $X$ на множество $Y$ ($X\times Y$) - это множество, элементами которого являются упорядоченные пары $⟨x,y⟩$ для всевозможных $x\in X$ и $y\in Y$. Упорядоченную пару, образованную из элементов $x$ и $y$, принято записывать, используя круглые скобки: $(x,y)$. Элемент $x$ называют первой координатой (компонентой) пары, а элемент $y$ - второй координатой (компонентой) пары. Всевозможные точки на плоскости в декартовой системе координат - это элементы декартова произведения множеств $X$ и $Y$ ($X\times Y$).

Предположим, что множества $X$ и $Y$ равны, то есть $X=Y=A$, где $A$ - множество целых неотрицательных чисел. В этом случае всевозможные точки на плоскости в декартовой системе координат - это элементы двукратного декартова произведения множества $A$ на себя ($A^2$).

Теперь рассмотрим декартову систему координат для трёхмерного пространства.

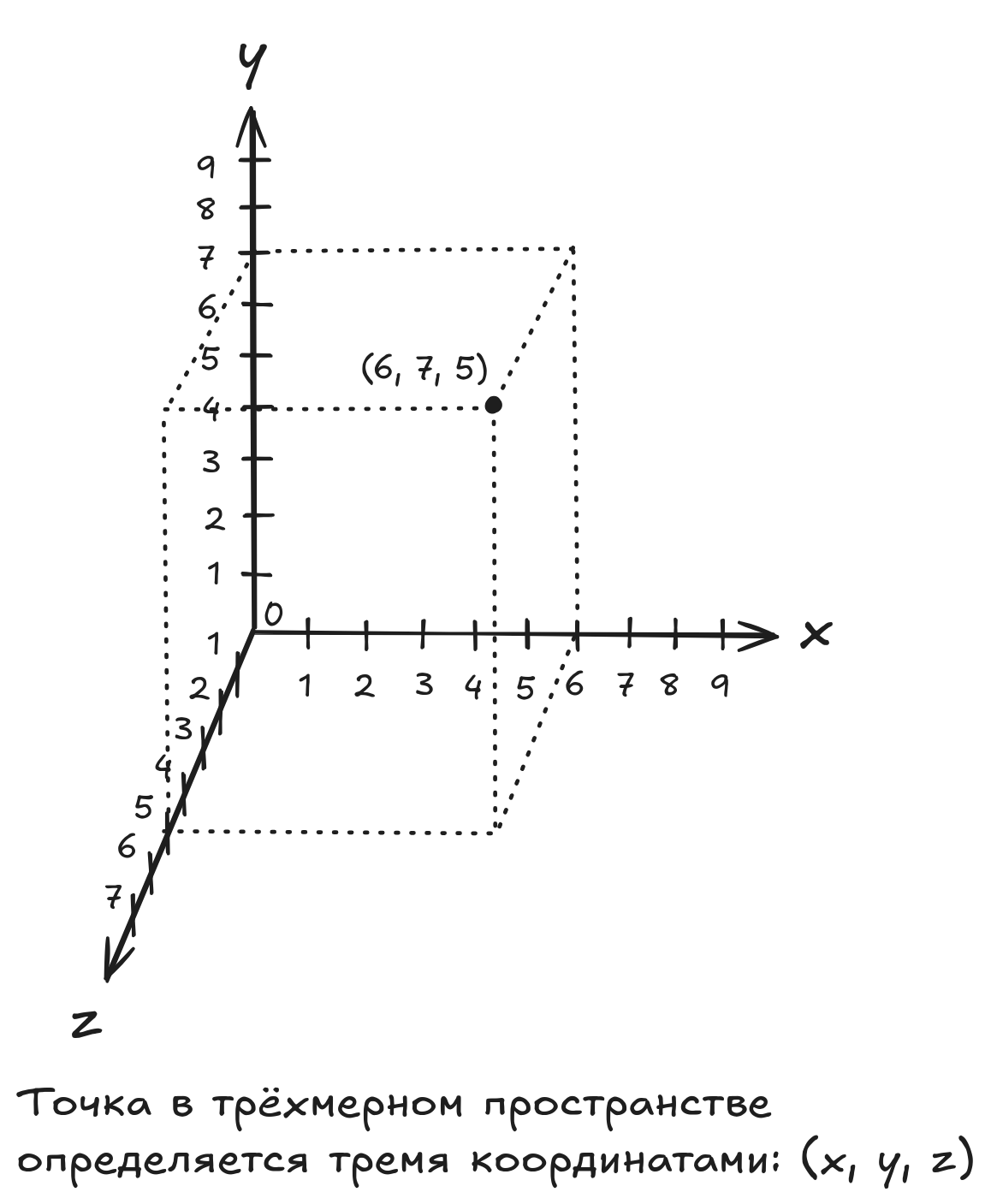
Пусть даны три множества $X$, $Y$ и $Z$. Декартово произведение трёх множеств $X$, $Y$ и $Z$ ($X\times Y\times Z$) - это множество, элементами которого являются упорядоченные тройки $⟨x,y,z⟩$ для всевозможных $x\in X$, $y\in Y$ и $z\in Z$. Всевозможные точки трёхмерного пространства в декартовой системе координат - это элементы декартова произведения множеств $X$, $Y$ и $Z$ ($X\times Y\times Z$). Упорядоченные тройки, образованные из элементов $x$, $y$ и $z$, также принято записывать, используя круглые скобки: $(x,y,z)$.

Предположим, что множества $X$, $Y$ и $Z$ равны, то есть $X=Y=Z=A$, где $A$ - множество целых неотрицательных чисел. В этом случае всевозможные точки трёхмерного пространства в декартовой системе координат - это элементы трёхкратного декартова произведения множества $A$ на себя ($A^3$).

Если мы будем продолжать увеличивать $n$-ю декартову степень множества $A$, то тем самым мы просто будем делать интересующее нас пространство более многомерным, но суть проводимых исследований при этом никак не изменится, мы всё так же будем рассматривать положения элементов (из декартова произведения $A^n$) в декартовой системе координат для $n$-мерного пространства.

---

ВПЕРЁД ⇒

Отношение с n аргументами на множестве

⇐ НАЗАД

Задание множества при помощи его элементов

---

Источники

• Э. Мендельсон “Введение в математическую логику”. Глава 0 “Введение” (стр. 7-18).
• Декартово-произведение (Wiki)

Категория

Математическая-логика Математическая-логика

Теги

• Логика Логика
• Множество Множество
• Элемент-множества Элемент-множества
• Пара Пара
• Неупорядоченная-пара Неупорядоченная-пара
• Упорядоченная-пара Упорядоченная-пара
• Декартово-произведение Декартово-произведение
• Декартова-степень Декартова-степень
• Упорядоченная-n-ка Упорядоченная-n-ка
• Одноэлементное-множество Одноэлементное-множество