16. Функции и отображения

---

ВПЕРЁД ⇒

Взаимно однозначные функции

⇐ НАЗАД

Классы R-эквивалентности

---

Функции и отображения

Бинарное отношение $f$ называется функцией, если из $⟨x,y⟩\in f$ и $⟨x,z⟩\in f$ следует $y=z$.

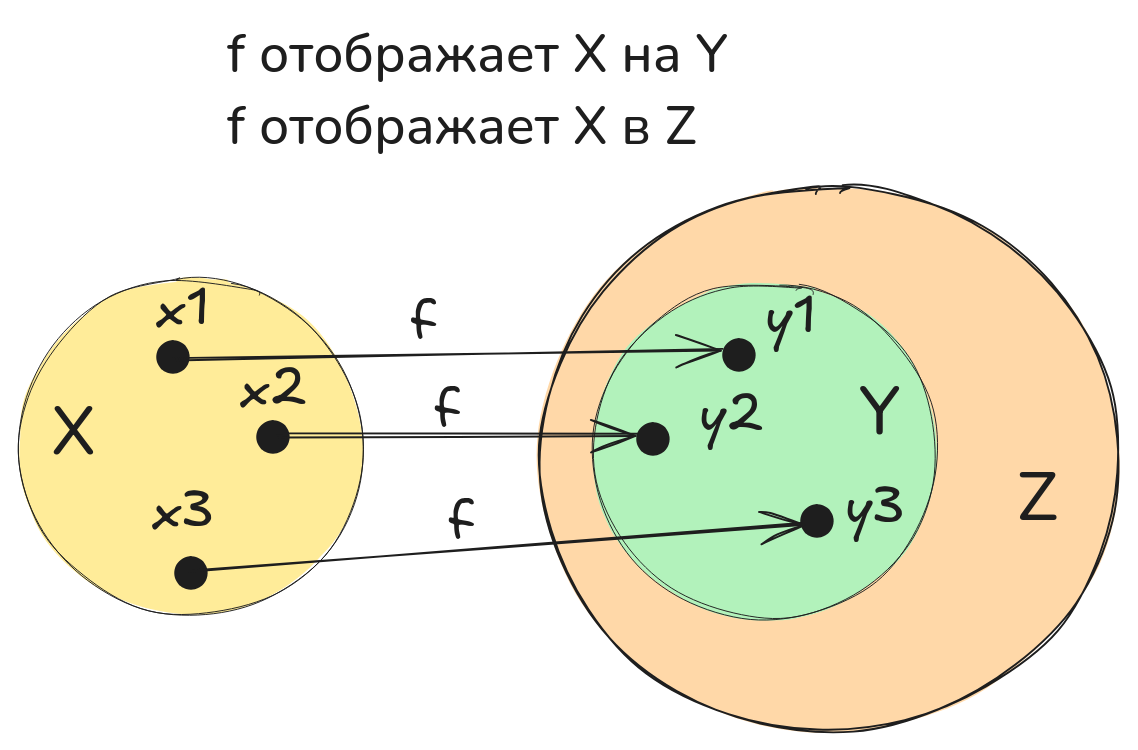
Для любого $x$ из области определения функции $f$ существует единственный элемент $y$ такой, что $⟨x,y⟩\in f$. Этот элемент $y$ обозначается через $f(x)$. Если $x$ принадлежит области определения $f$, то говорят, что $f(x)$ определено. Если $f$ является функцией с областью определения $X$ и множеством значений $Y$, то говорят, что $f$ отображает $X$ на $Y$. Если $f$ отображает $X$ на $Y$ и $Y\subseteq Z$, то говорят, что $f$ отображает $X$ в $Z$.

Например, если функция $f(x)=2x$ определена для любого целого $x$, то мы можем сказать, что $f$ отображает множество всех целых чисел на множество всех чётных чисел. С другой стороны, множество всех чётных чисел - это подмножество множества всех целых чисел. Поэтому мы можем сказать, что $f$ отображает множество всех целых чисел в множество всех целых чисел.

Функция, область определения которой состоит из $n$-ок, называется функцией от $n$ аргументов:

$⟨z,y⟩\in f$, где $z\in X^n$ и $y\in Y$

На место $z$ подставим упорядоченную $n$-ку из множества $X^n$:

$⟨⟨x_1,...,x_n⟩,y⟩\in f$, где $⟨x_1,...,x_n⟩\in X^n$ и $y\in Y$

Перепишем в следующем виде:

$y=f(⟨x_1,...,x_n⟩)$, где $⟨x_1,...,x_n⟩\in X^n$ и $y\in Y$

Обычно вместо выражения "$y=f(⟨x_1,...,x_n⟩)$" пишут "$y=f(x_1,...,x_n)$".

Всюду определённой функцией от n аргументов на множестве X называется любая функция, у которой область определения совпадает с $X^n$ ($n$-кратным декартовым произведением множества $X$ на себя).

Частичной функцией от n аргументов на множестве X называется любая функция, областью определения которой служит какое-нибудь подмножество множества $X^n$. Например, обычное деление $f(x,y)=\frac{x}{y}$ является частично (не всюду) определенной функцией от двух аргументов на множестве целых чисел, поскольку деление на нуль не определено.

Пусть имеется функция $f$ с областью определения $X$ и множеством значений $Y$. Тогда, ограничением функции f множеством Z называется функция $f_Z=f\cap (Z\times Y)$.

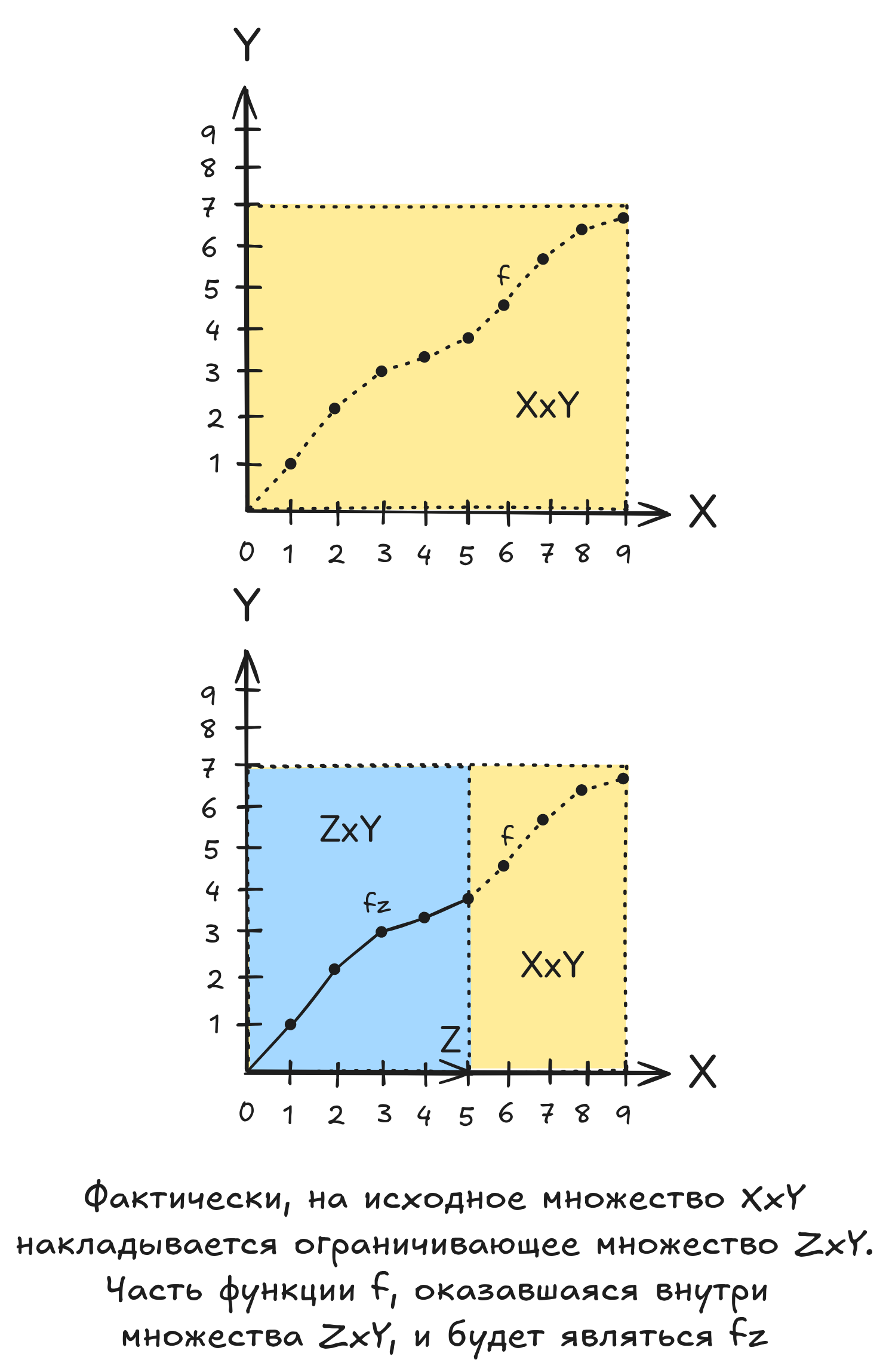
Ограничение функции f множеством Z представляет собой ограничение исходного множества $X$ (то есть исходной области определения функции) некоторым множеством $Z$. Новая область определения находится как $X^{\prime }=X\cap Z$. Очевидно, что $f_Z(u)=v$ тогда и только тогда, когда $u\in Z$ и $f(u)=v$.

Образом множества Z при отображении посредством функции f называется множество значений функции $f_Z$. Иначе говоря, из исходной области определения функции выбирается только та часть, которая попадает в $Z$, и для полученной таким образом новой области определения берутся все соответствующие ей значения функции $f$, которые и составляют образ множества $Z$.

Прообразом множества W при отображении посредством функции f называется множество всех тех элементов $u$ из области определения функции $f$, для которых $f(u)\in W$. Из определения следует, что прообраз множества W при отображении посредством функции f есть не что иное, как множество значений обратного отношения $g=f^{-1}$, областью определения которого является $W$. Обратите внимание на то, что мы зовём $g$ отношением (обратным к $f$), а не функцией (обратной к $f$), поскольку обратные отношения могут и не быть функциями (см. пример далее).

$$\begin{array}{r}⟨x_1,a⟩\in f,\\ ⟨x_2,b⟩\in f,\\ ⟨x_3,b⟩\in f,\\ ⟨x_4,c⟩\in f.\\ ⟨a,x_1⟩\in f^{-1},\\ ⟨b,x_2⟩\in f^{-1},\\ ⟨b,x_3⟩\in f^{-1},\\ ⟨c,x_4⟩\in f^{-1}.\end{array}$$

В представленном выше примере отношение $f$ является функцией, поскольку для любого $x$ из области определения функции $f$ существует единственный элемент $y$ такой, что $⟨x,y⟩\in f$. В обратном же отношении $f^{-1}$ одному элементу $b$ из области определения бинарного отношения $f^{-1}$ соответствуют сразу два элемента из множества значений этого же бинарного отношения, следовательно $f^{-1}$ функцией не является.

Говорят, что функция f отображает множество X на множество Y, если $X$ является подмножеством области определения $f$, а образом $X$ при отображении посредством $f$ является множество $Y$.

Говорят, что функция f отображает множество X в множество Y, если $X$ является подмножеством области определения $f$, а образом $X$ при отображении посредством $f$ является подмножество множества $Y$.

Под n-местной операцией (или операцией с n аргументами) на множестве X подразумевается функция, отображающая $X^n$ в $X$:

$⟨⟨x_1,...,x_n⟩,y⟩\in f$, где $⟨x_1,...,x_n⟩\in X^n$ и $y\in X$

Например, обычное сложение является бинарной (двуместной) операцией на множестве целых неотрицательных чисел $X=\{0,1,2,...\}$:

$⟨⟨x_1,...,x_n⟩,y⟩\in +$, где $⟨x_1,...,x_n⟩\in X^n$ и $y\in X$

Напротив, обычное вычитание не является бинарной операцией на множестве целых неотрицательных чисел, так как разность между двумя целыми неотрицательными числами может быть отрицательной. По этой причине в вычитании рассматривают не целые неотрицательные числа, а просто целые числа. Таким образом, обычное вычитание является бинарной операцией на множестве всех целых чисел.

$⟨⟨x_1,...,x_n⟩,y⟩\in -$, где $⟨x_1,...,x_n⟩\in X^n$ и $y\in X$

---

ВПЕРЁД ⇒

Взаимно однозначные функции

⇐ НАЗАД

Классы R-эквивалентности

---

Источники

• Э. Мендельсон “Введение в математическую логику”. Глава 0 “Введение” (стр. 7-18).

Категория

Математическая-логика Математическая-логика

Теги

• Логика Логика
• Множество Множество
• Отношение Отношение
• Упорядоченная-n-ка Упорядоченная-n-ка
• n-местное-отношение n-местное-отношение
• Отношение-с-n-аргументами Отношение-с-n-аргументами
• Бинарное-отношение Бинарное-отношение
• Двуместное-отношение Двуместное-отношение
• Обратное-отношение Обратное-отношение
• Область-определения Область-определения
• Множество-значений Множество-значений
• Функция Функция
• Обратная-функция Обратная-функция
• Отображение Отображение
• Операция Операция
• n-местная-операция n-местная-операция
• Операция-с-n-аргументами Операция-с-n-аргументами
• Бинарная-операция Бинарная-операция
• Двуместная-операция Двуместная-операция
• Образ-множества Образ-множества
• Прообраз-множества Прообраз-множества
• Ограничение-функции-множеством Ограничение-функции-множеством
• Функция-от-n-аргументов Функция-от-n-аргументов
• Всюду-определённая-функция Всюду-определённая-функция
• Частичная-функция Частичная-функция