17. Взаимно однозначные функции

---

ВПЕРЁД ⇒

Композиция функций

⇐ НАЗАД

Функции и отображения

---

Взаимно однозначные функции

Определение взаимно однозначной функции

Функция $f$, для которой из $f(x)=f(y)$ следует $x=y$, называется взаимно однозначной функцией (или функцией "один в один", то есть функцией, одному значению которой соответствует ровно одно значение её аргумента). Также говорят, что во взаимно однозначной функции любому элементу из области определения функции поставлен во взаимно однозначное соответствие свой собственный элемент из множества значений этой функции.

Примеры взаимно однозначных функций

• Отношение тождества $I_X$ на множестве $X$. Для отношения тождества $R$ множество $X$ разбивается на $n$ различных классов $R$-эквивалентности, представляющих собой одноэлементные множества $\{x_k\}$, где $k\in \{1,...,n\}$ (см. “Классы R-эквивалентности”). Это означает, что отношение тождества $⟨z,z⟩\in I_X$, $z\in X$ состоит из $n$ уникальных упорядоченных пар $⟨z,z⟩=⟨z,I_X(z)⟩$, что и показывает наличие взаимно однозначного соответствия между $z$ и $I_X(z)$. Иными словами, в отношении тождества каждый элемент множества поставлен во взаимно однозначное соответствие самому себе.
• Любая линейная функция $f(x)=kx$ для любого произвольного числа $x$.

Заметим, что любая квадратичная функция $f(x)=k{x}^2$ не является взаимно однозначной, поскольку, например, $f(-1)=f(1)=k$.

Обратные функции

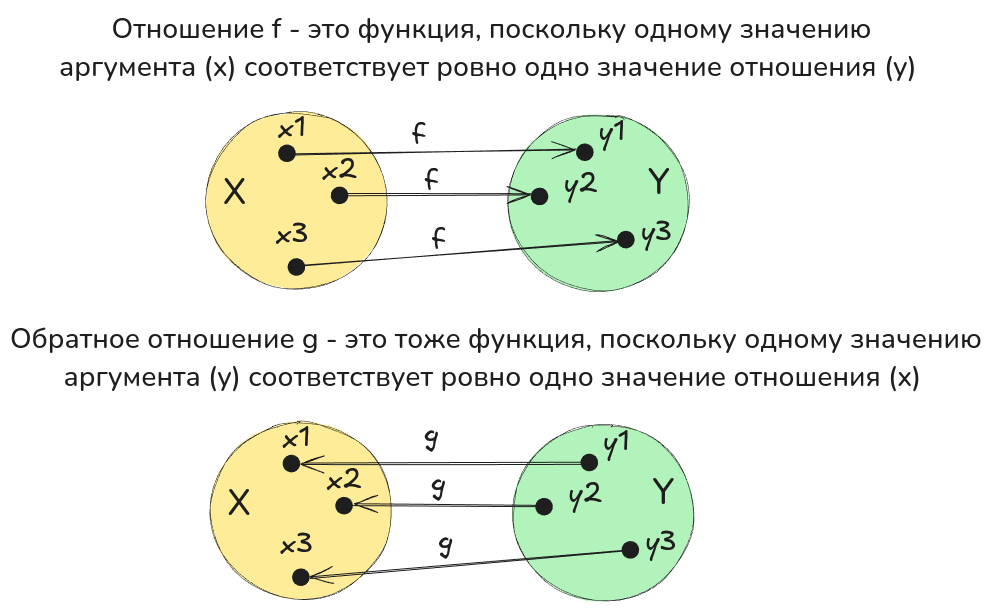
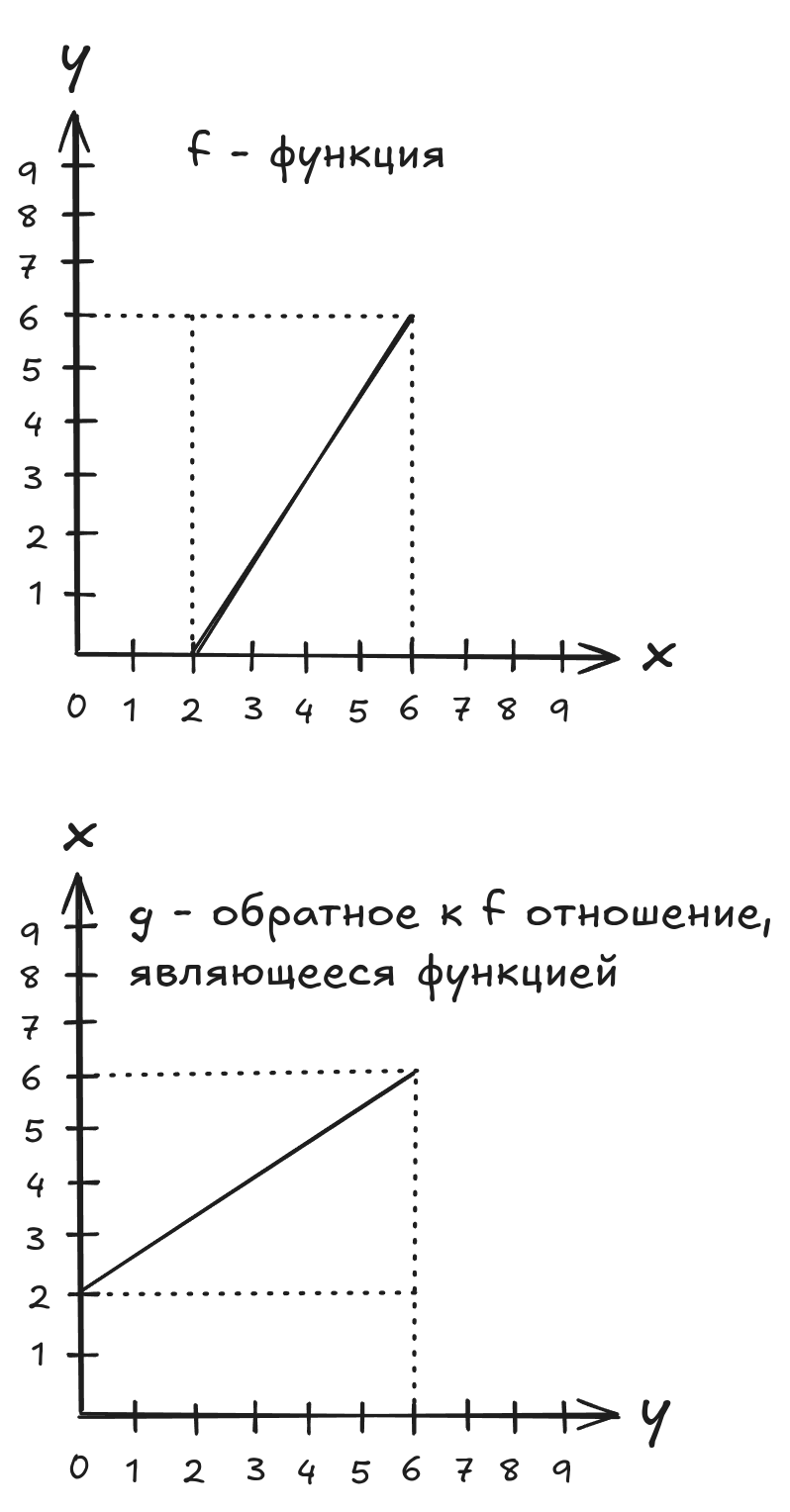
Из иллюстраций ниже следует, что функция $f$ является взаимно однозначной тогда и только тогда, когда обратное отношение $g=f^{-1}$ тоже является функцией. Иными словами, обратные функции бывают только у взаимно однозначных функций.

Взаимно однозначная функция и обратная ей функция:

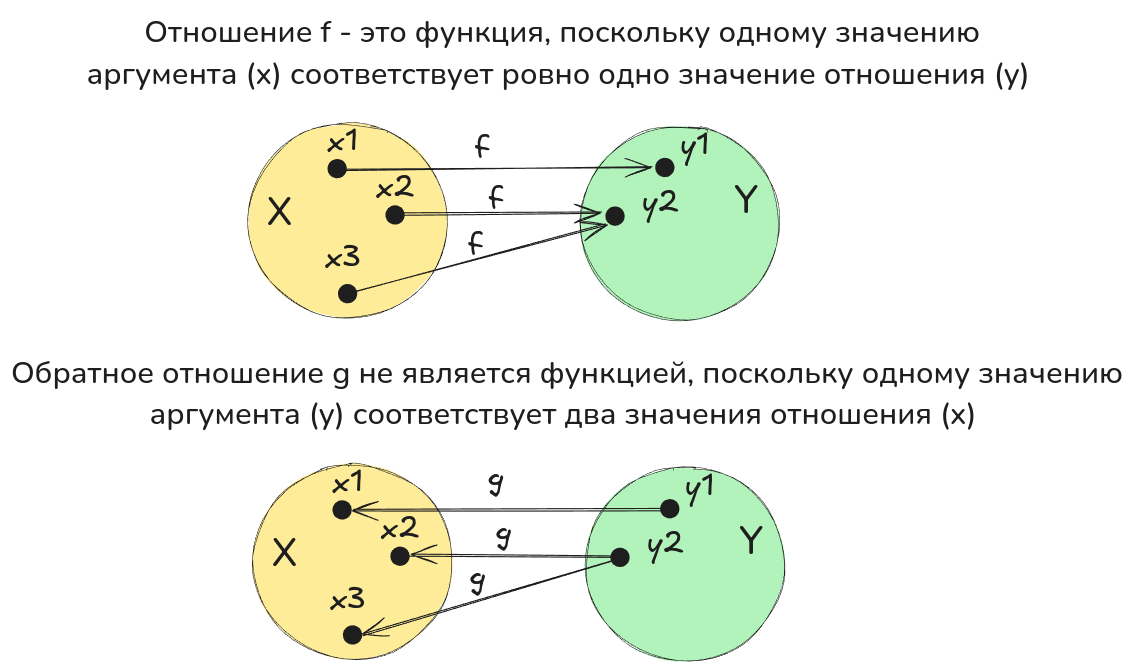
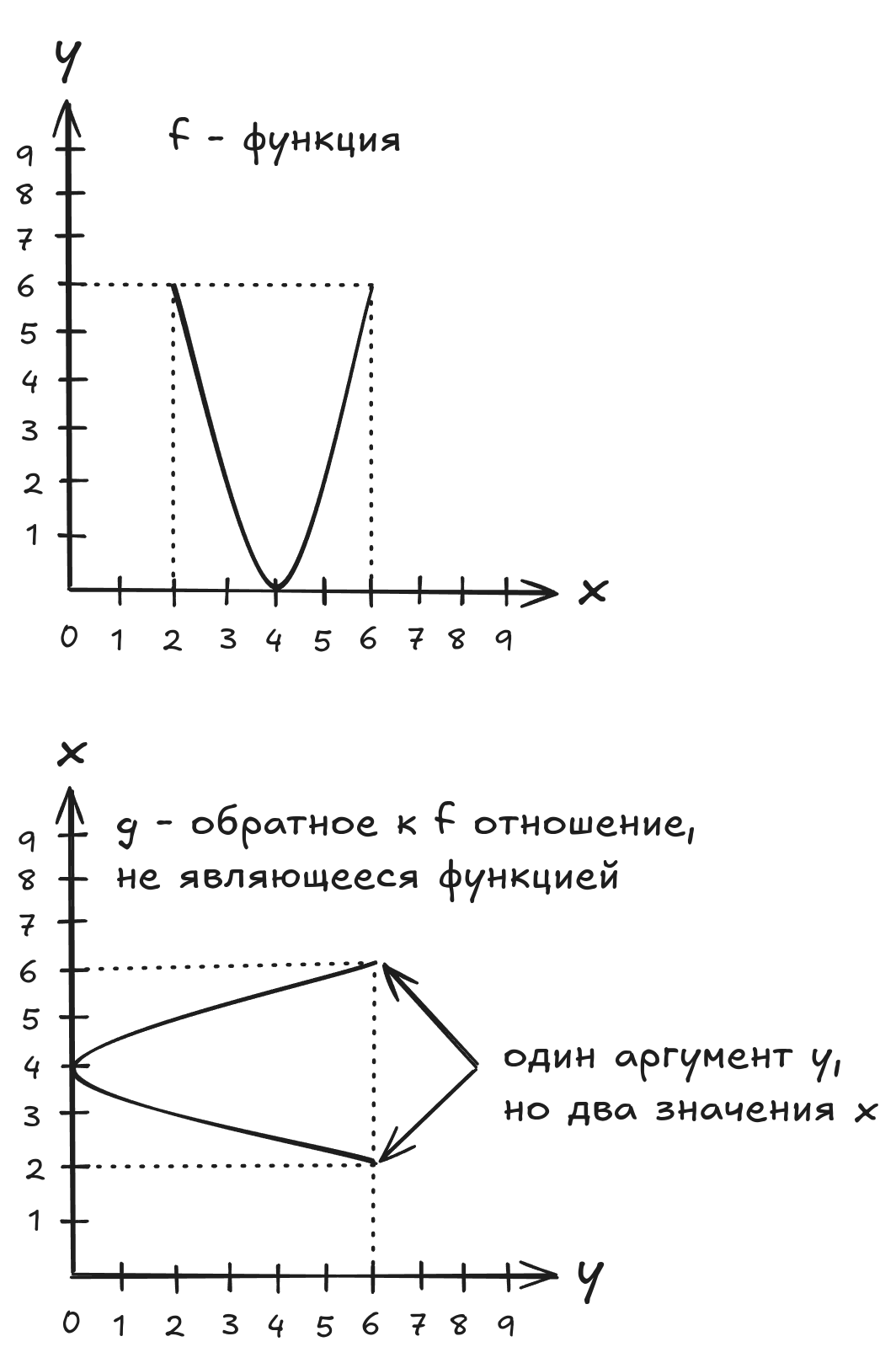
Не взаимно однозначная функция и обратное отношение к ней:

Предположим, что функция $f^{-1}$ является обратной к функции $f$. С одной стороны, из этого следует, что $f$ - взаимо однозначная функция, поскольку обратные функции бывают только у взаимно однозначных функций. С другой стороны, функция $f$ также является обратной к функции $f^{-1}$, и отсюда точно так же следует, что $f^{-1}$ тоже является взаимно однозначной функцией. Таким образом, можем сделать окончательный вывод, что если для функции $f$ существует обратная ей функция $f^{-1}$, то обе функции $f$ и $f^{-1}$ являются взаимно однозначными.

Взаимно однозначное соответствие между множествами

Если $X$ является областью определения, а $Y$ - множеством значений взаимно однозначной функции $f$, то о функции $f$ говорят, что она является взаимно однозначным соответствием (или соответствием "один в один") между множествами $X$ и $Y$. При этом обратная функция $f^{-1}$ оказывается взаимно однозначным соответствием между $Y$ и $X$.

---

ВПЕРЁД ⇒

Композиция функций

⇐ НАЗАД

Функции и отображения

---

Источники

• Э. Мендельсон “Введение в математическую логику”. Глава 0 “Введение” (стр. 7-18).

Категория

Математическая-логика Математическая-логика

Теги

• Логика Логика
• Множество Множество
• Функция Функция
• Взаимно-однозначная-функция Взаимно-однозначная-функция
• Взаимно-однозначное-соответствие Взаимно-однозначное-соответствие