15. Классы R-эквивалентности

---

ВПЕРЁД ⇒

Функции и отображения

⇐ НАЗАД

Отношение тождества

---

Классы R-эквивалентности

Пусть имеется отношение эквивалентности $R$ на множестве $X$, пусть также $y$ - некоторый элемент множества $X$. Определим множество $[y]$ как множество всех элементов $z$ из $X$ таких, что они находятся в отношении эквивалентности $R$ с элементом $y$, то есть $zRy$, где $z\in [y]$. Множество $[y]$ называется классом $R$-эквивалентности, определяемым элементом $y$.

Пусть имеются два множества: $[y]$ (класс $R$-эквивалентности, определяемый элементом $y$) и $[z]$ (класс $R$-эквивалентности, определяемый элементом $z$). Множества $[y]$ и $[z]$ равны ($[y]=[z]$, то есть классы $R$-эквивалентности равны) тогда и только тогда, когда элементы $y$ и $z$ находятся в отношении эквивалентности $R$ ($yRz$). Если $[y]\ne [z]$ (если классы $R$-эквивалентности не равны), то $[y]\cap [z]=0$ (то это означает, что они не имеют общих элементов).

Примеры классов R-эквивалентности

Классы R-эквивалентности для параллельных прямых

Простейшим примером классов $R$-эквивалентности являются наборы параллельных прямых в плоскости. В этом случае в один класс $R$-эквивалентности попадают прямые, имеющие одинаковую направленность на плоскости.

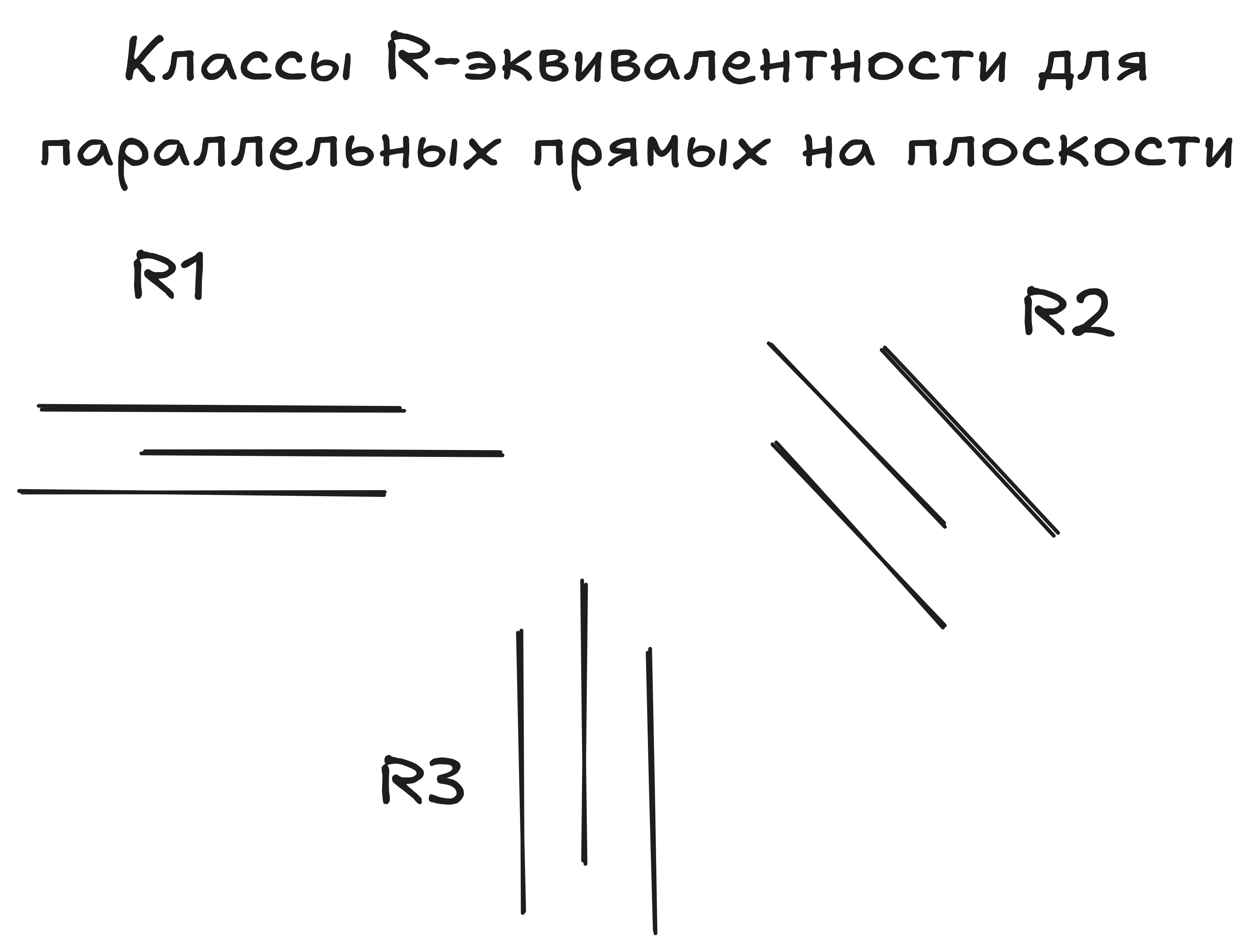
На изображении выше представлены 3 группы параллельных прямых (они же классы $R$-эквивалентности): $R1$, $R2$ и $R3$. Обозначим через $R{1}_1$, …, $R{1}_k$, $R{2}_1$, … , $R{2}_m$, $R{3}_1$, …, $R{2}_n$ прямые в этих группах/классах. Согласно определению класса $R$-эквивалентности каждую из групп можно обозначить следующими способами:

• $[R{1}_1]$ - множество параллельных прямых из группы $R1$, также это множество можно обозначить, к примеру, как $[R{1}_k]$.
• $[R{2}_1]$ - множество параллельных прямых из группы $R2$, также это множество можно обозначить, к примеру, как $[R{2}_m]$.
• $[R{3}_1]$ - множество параллельных прямых из группы $R3$, также это множество можно обозначить, к примеру, как $[R{2}_n]$.

Обратите внимание, поскольку элементы $R{1}_1$ и $R{1}_k$ находятся в отношении эквивалентности (параллельны друг другу), то из этого следует, что классы $R$-эквивалентности $[R{1}_1]$ и $[R{1}_k]$ совпадают (множества $[R{1}_1]$ и $[R{1}_k]$ равны друг другу). Одновременно с этим, классы $R$-эквивалентности $[R{1}_1]$ и $[R{3}_1]$ не равны друг другу (множества $[R{1}_1]$ и $[R{3}_1]$ не имеют общих элементов).

Классы R-эквивалентности для отношения тождества

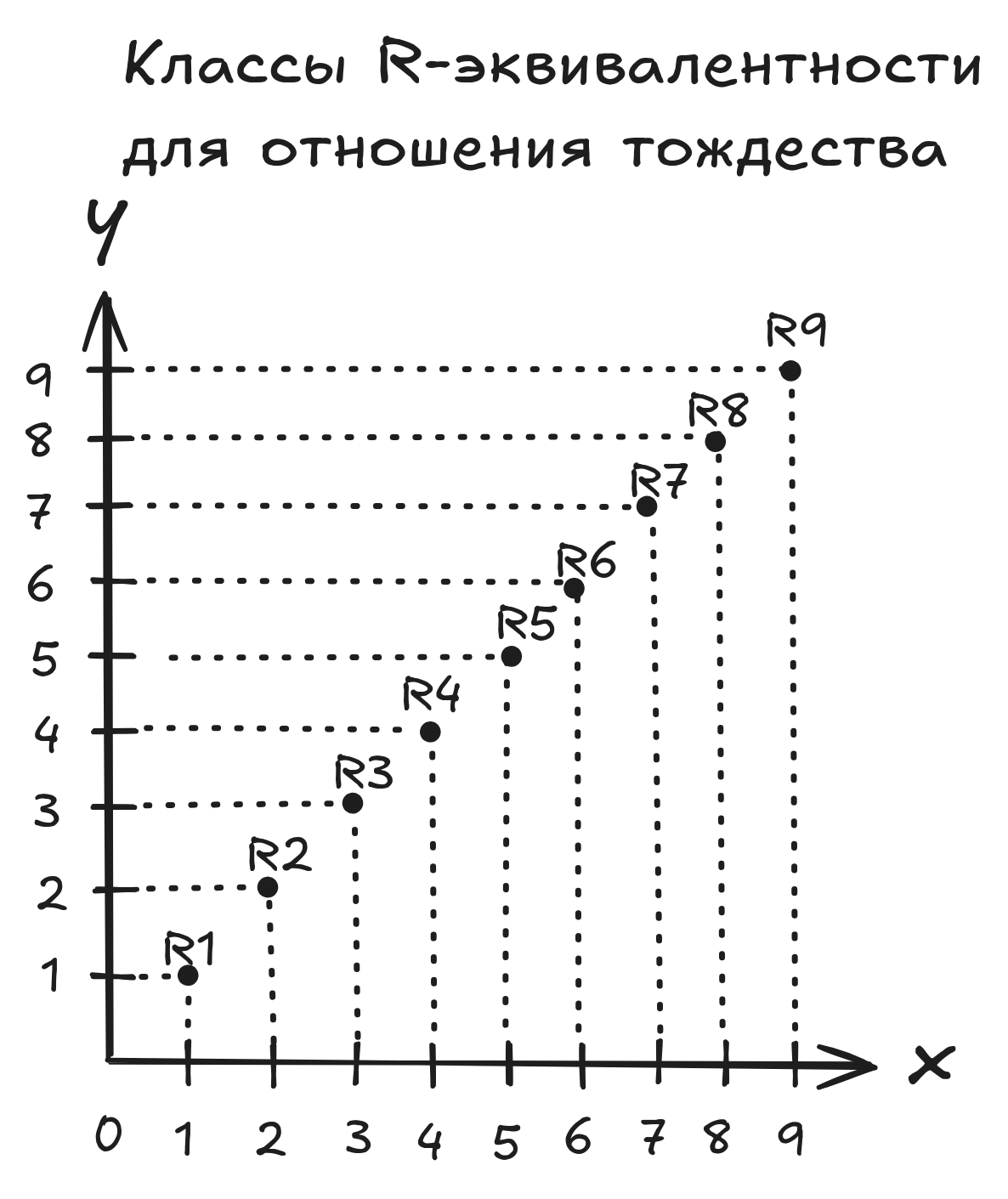
В качестве примера отношения эквивалентности $R$ на множестве $X=\{x_1,x_2,...,x_n\}$ рассмотрим отношение тождества $I_X$ ($z\equiv y$). Для любого произвольного множества $X=\{x_1,x_2,...,x_n\}$ отношение тождества можно записать как ”$⟨z,z⟩\in \equiv$, $z\in X$“. Для отношения тождества $R$ множество $X$ разбивается на $n$ различных классов $R$-эквивалентности, представляющих собой одноэлементные множества $\{x_k\}$, где $k\in \{1,...,n\}$. Это можно доказать так:

Если предположить, что в отношении тождества на множестве из $n$ элементов количество различных классов $R$-эквивалентности меньше $n$, то это означает, что есть как минимум один класс $R$-эквивалентности с двумя элементами $x_i$ и $x_j$ такими, что $⟨x_i,x_j⟩\in \equiv$, $z\in X$. Но, согласно определению отношения тождества, в нём могут быть только упорядоченные пары $⟨x_i,x_i⟩\in \equiv$ и $⟨x_j,x_j⟩\in \equiv$, но не $⟨x_i,x_j⟩\in \equiv$. Более того, мы должны помнить о том, что множества не содержат дублирующихся элементов. Если бы мы рассматривали множество $\{x_i,x_k\}$, и при этом выполнялось условие $x_i\equiv x_k$, то это бы значило, что $\{x_i,x_k\}=\{x_i,x_i\}=\{x_i\}$, то есть нами бы рассматривался один и тот же элемент множества, поскольку в множестве не может существовать двух и более одинаковых (неотличимых) элементов. Но тогда бы это противоречило нашему исходному предположению о том, что в одном из классов $R$-эквивалентности присутствует как минимум два дублирующихся элемента $x_i$ и $x_k$. Значит, наше исходное предположение неверно, откуда следует, что для отношения тождества $R$ ($\equiv$) множество $X=\{x_1,x_2,...,x_n\}$ может быть разбито только на $n$ классов $R$-эквивалентности.

---

ВПЕРЁД ⇒

Функции и отображения

⇐ НАЗАД

Отношение тождества

---

Источники

• Э. Мендельсон “Введение в математическую логику”. Глава 0 “Введение” (стр. 7-18).

Категория

Математическая-логика Математическая-логика

Теги

• Логика Логика
• Множество Множество
• Элемент-множества Элемент-множества
• Отношение Отношение
• Тождество Тождество
• Отношение-тождества Отношение-тождества
• Эквивалентность Эквивалентность
• R-эквивалентность R-эквивалентность
• Класс-R-эквивалентности Класс-R-эквивалентности