08. Множества

---

ВПЕРЁД ⇒

Задание множества при помощи его элементов

⇐ НАЗАД

Логические связки утверждений

---

Множества

Определение множества

Вернёмся к примеру с кирпичиками из набора конструктора лего. В примере для построения одной игрушки требуется 100 кирпичиков, двух игрушек - 200 кирпичиков, трёх игрушек - 300 кирпичиков, и т.д. Таким образом, про область изменения величины $x$ (числа используемых кирпичиков) можно сказать, что она представляет собой совокупность целых неотрицательных чисел, кратных 100, то есть областью изменения $x$ является множество.

Множество - совокупность (собрание) объектов. Любой объект этого собрания называется элементом множества.

В графическом виде (на бумаге или на дисплее монитора) множества, их элементы, а также пересечения множеств (когда множества обладают общими элементами) обозначают при помощи диаграмм Эйлера, то есть при помощи геометрических схем (кругов или иных фигур), являющихся интуитивно понятными любому читателю (см. примеры ниже).

Принадлежность элементов множеству

Пусть $y$ - множество, а $x$ - элемент множества $y$. Тогда для обозначения того факта, что $x$ принадлежит (является элементом) $y$, используется запись "$x\in y$".

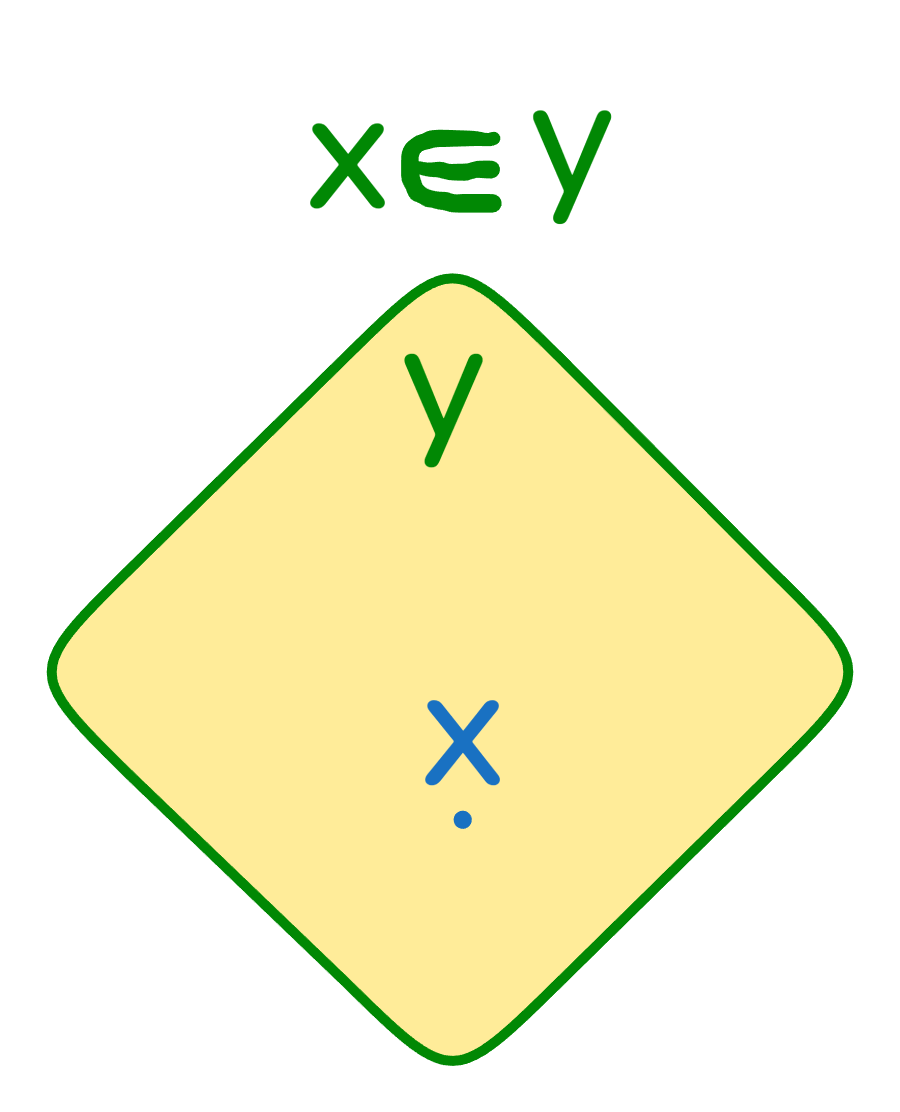
Если мы хотим сказать, что $x$ не принадлежит (не является элементом) $y$, то нам необходимо использовать запись "$x\notin y$".

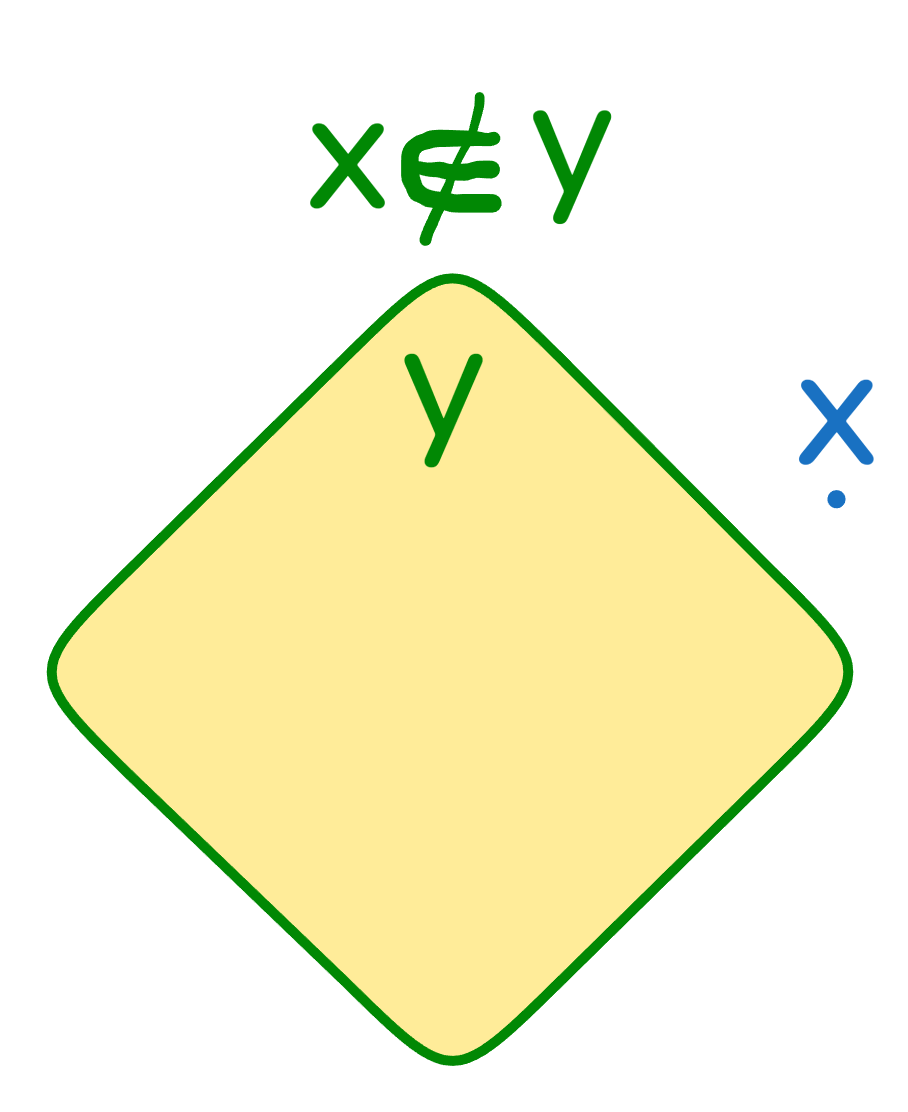
Подмножества

Пусть теперь $x$ и $y$ - множества, а все элементы множества $x$ также являются элементами множества $y$. Причём $y$ может как содержать дополнительные элементы, не входящие в $x$, так и не содержать никаких дополнительных элементов. В этом случае говорят, что $x$ является подмножеством $y$. На самом деле, правильней было бы говорить, что $x$ является нестрогим подмножеством $y$. Однако, на практике, обычно используют указанный сокращённый вариант ($x$ является подмножеством $y$). Так поступают по причине того, что кроме термина "нестрогое подмножество" также существует отдельный термин "собственное подмножество", использующийся для обозначения строгих подмножеств (более подробное описание собственных подмножеств представлено ниже), и если в термине "нестрогое подмножество" мы опустим слово "нестрогое", то это не будет являться сильно критичным для нас, поскольку, благодаря наличию выделенного термина для обозначения строгих подмножеств, мы всегда будем понимать, какой тип подмножеств подразумевается в тексте. Для того, чтобы показать, что $x$ является подмножеством $y$, необходимо использовать запись "$x\subseteq y$". Символ "$\subseteq$" является комбинацией двух символов: "$\subset$" (строгого подмножества) и "$=$" (равного множества),- то есть таким образом подчёркивается момент, что нам без разницы, содержит ли $y$ (или нет) дополнительные элементы, не входящие в $x$.

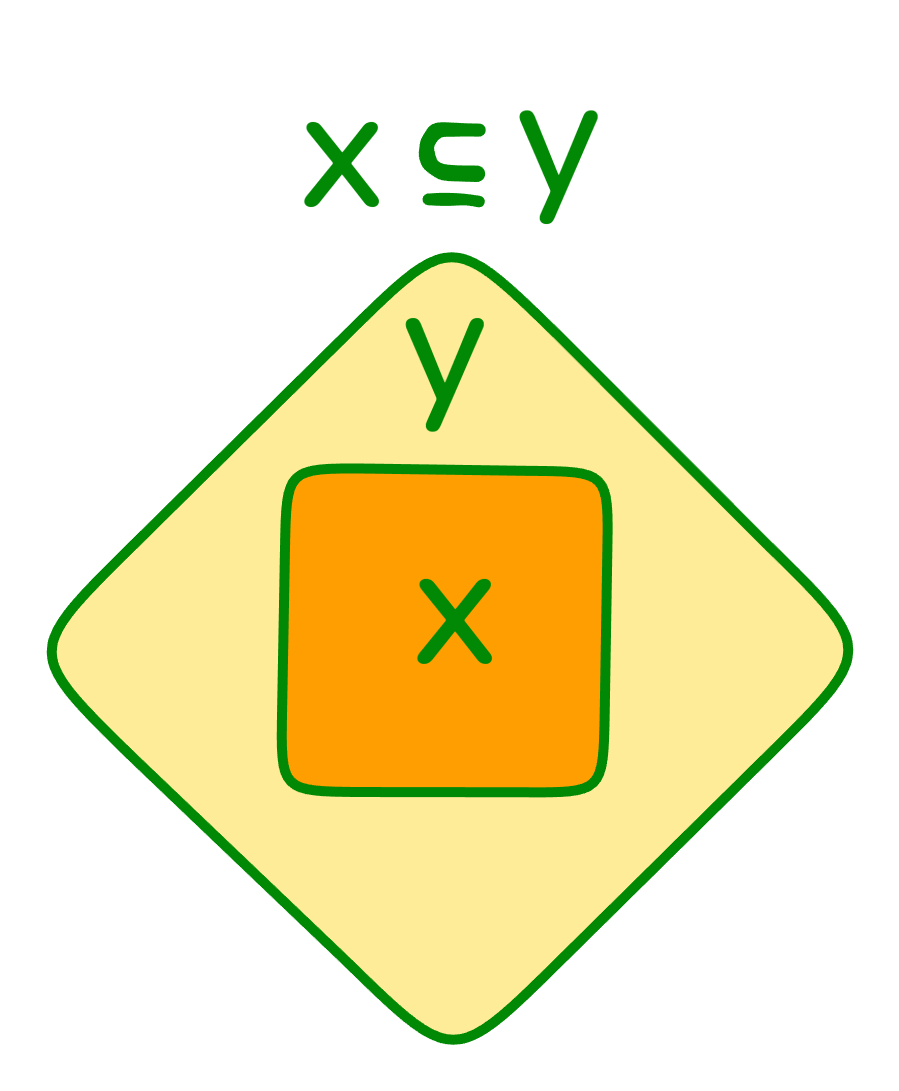
Однако, если мы знаем, что все элементы множества $x$ в точности совпадают со всеми элементами множества $y$ (то есть $x$ и $y$ являются равными множествами), и хотим подчеркнуть этот момент, то вместо "$x\subseteq y$" мы обычно пишем "$x=y$". Аналогично, если нам известно, что множество $y$, кроме всех элементов множества $x$, также включает в себя и другие элементы, не входящие в множество $x$, и мы хотим подчеркнуть этот момент, то мы говорим, что множество $x$ является собственным подмножеством множества $y$ и используем запись "$x\subset y$" вместо записи "$x\subseteq y$" (то есть, как можно видеть, вместо термина "строгое подмножество" обычно используется термин "собственное подмножество"). При этом отметим, что два множества $x$ и $y$ являются равными в том и только в том случае, если "$x\subseteq y$" и "$y\subseteq x$".

Объединение множеств

Объединение множеств $x$ и $y$ (записывается как "$x\cup y$") - это множество всех объектов, являющихся элементами хотя бы одного из множеств $x$ и $y$.

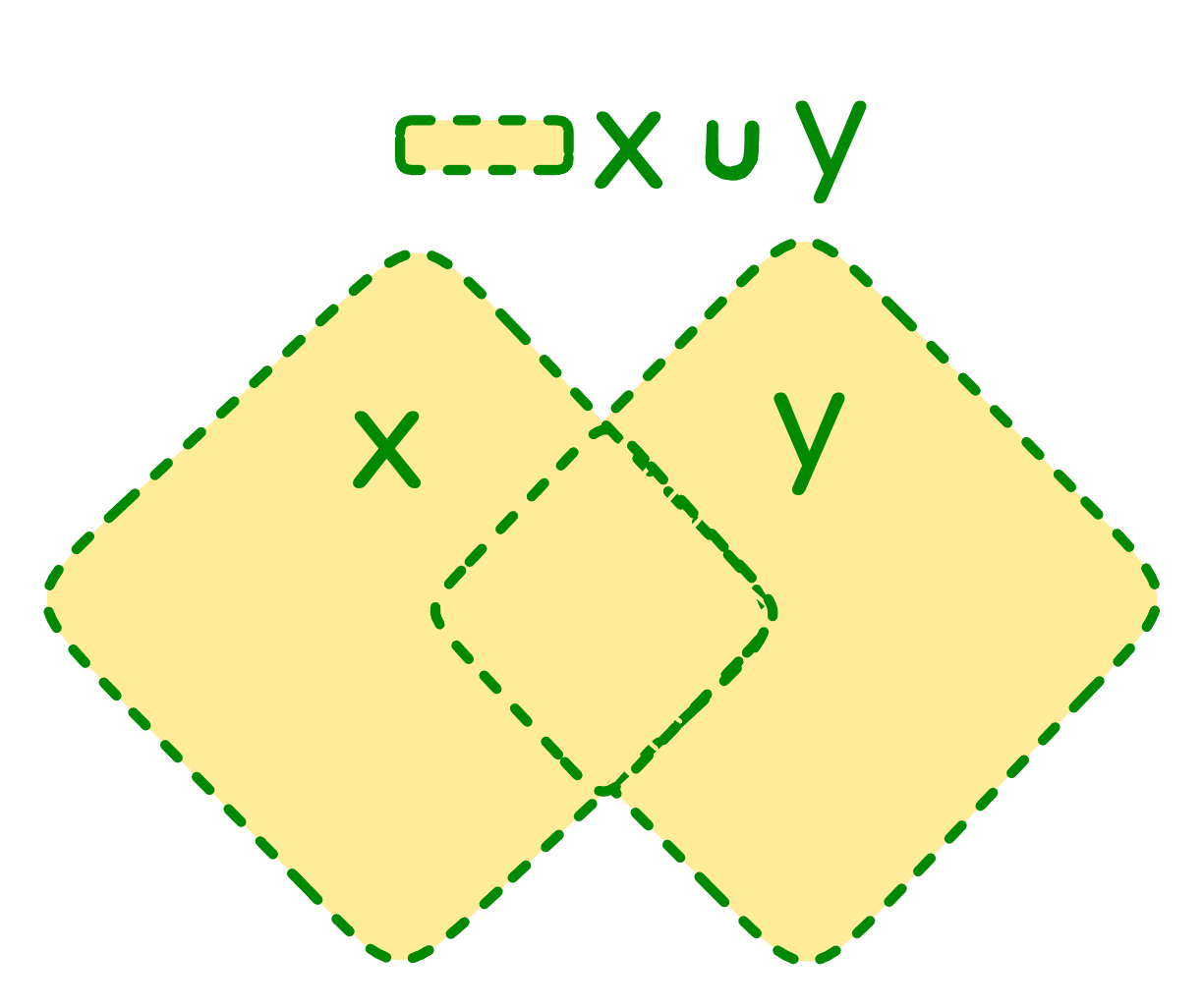
Для объединения множеств справедливы формулы:

$$\begin{array}{rl}x\cup x& =x\\ x\cup y& =y\cup x\\ (x\cup y)\cup z& =x\cup (y\cup z)\end{array}$$

Пересечение множеств

Пересечение множеств $x$ и $y$ (записывается как "$x\cap y$") - это множество всех объектов, одновременно принадлежащих и $x$, и $y$.

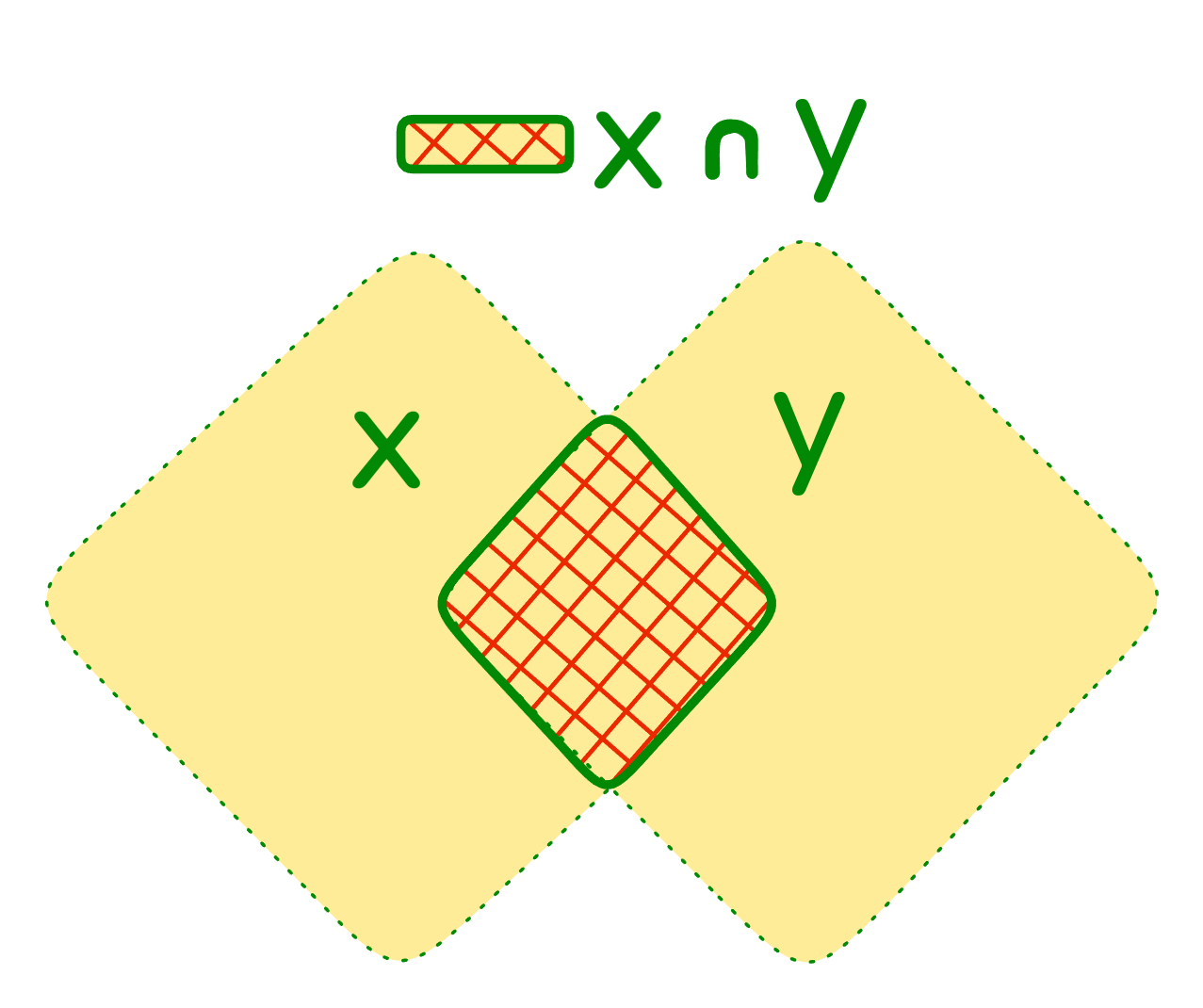
Для пересечения множеств справедливы формулы:

$$\begin{array}{rl}x\cap x& =x\\ x\cap y& =y\cap x\\ (x\cap y)\cap z& =x\cap (y\cap z)\\ x\cap (y\cup z)& =(x\cap y)\cup (x\cap z)\\ x\cup (y\cap z)& =(x\cup y)\cap (x\cup z)\end{array}$$

Разность множеств

Разность (относительное дополнение) множеств $x$ и $y$ (записывается как "$x-y$") - это множество тех элементов $x$, которые не являются элементами $y$.

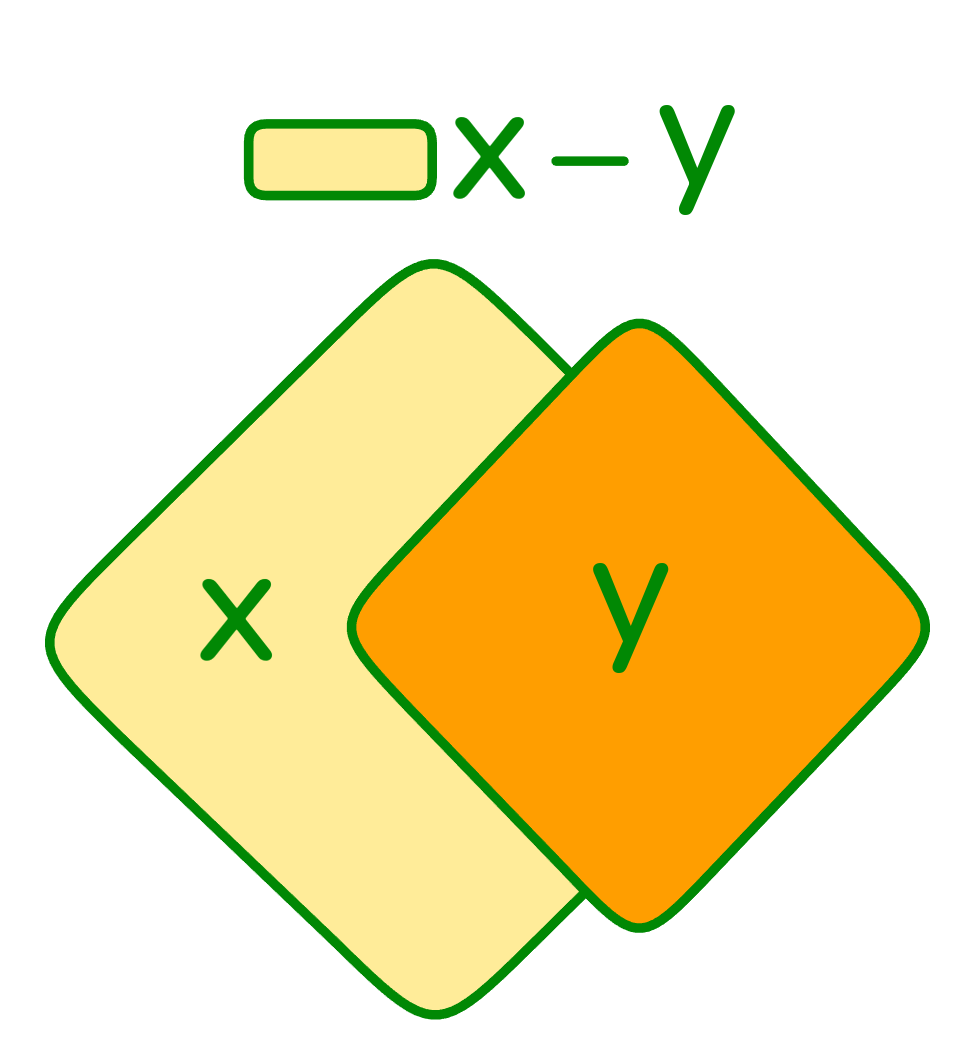
Пустое множество

Пустое множество (множество $0$) - множество, не имеющее элементов.

Два множества $x$ и $y$ называются непересекающимися множествами, если "$x\cap y=0$".

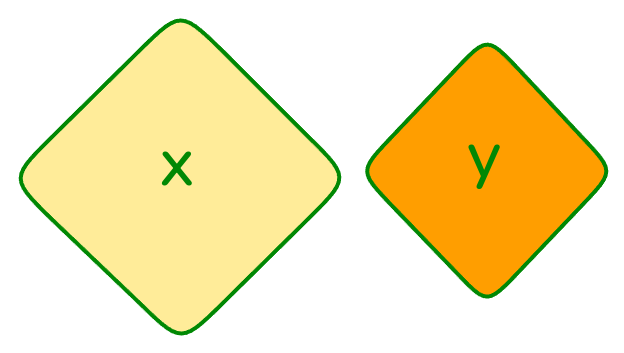
Для пустого множества справедливы формулы:

$$\begin{array}{rl}x\cap 0& =0\\ x\cup 0& =x\\ x-0& =x\\ x-x& =0\end{array}$$

---

ВПЕРЁД ⇒

Задание множества при помощи его элементов

⇐ НАЗАД

Логические связки утверждений

---

Источники

• Э. Мендельсон “Введение в математическую логику”. Глава 0 “Введение” (стр. 7-18).
• Диаграмма Эйлера (Wiki)

Категория

Математическая-логика Математическая-логика

Теги

• Логика Логика
• Переменная Переменная
• Множество Множество
• Область-изменения Область-изменения
• Подмножество Подмножество
• Элемент-множества Элемент-множества
• Объединение-множеств Объединение-множеств
• Пересечение-множеств Пересечение-множеств
• Относительное-дополнение Относительное-дополнение
• Разность-множеств Разность-множеств
• Пустое-множество Пустое-множество
• Диаграмма-Эйлера Диаграмма-эйлера